2 sqrt(3) times the width of the cube, then it completely engulfs the cube and the intersection of the 2 objects is just the volume of a cube. In between, I've found it looks like this:
The gray vertical lines represent when to use which equation. There are in fact 2 other regimes besides the two I discussed. I'm going to discuss these regimes as related to the ratio of the
rho and d where the first is the radius of the sphere and the second is half the cube width. Let's see them visually.The first regime is the spherical, where
rho / d < 1. It looks like a sphere:
The second regime has circular "lenses" cut-off from the sphere and occurs while
rho / d < sqrt(2):The third regime is characterized by filling the 8 corners of the cube:
Finally, the last regime is just a cube. This occurs at
rho / d > sqrt(3):
We can use those rotation transformation we learned in calculus. That is described by the equation:
The last regime is much more difficult to deal with. The sphere is first broken into 16ths and then each piece of that is divided into 5 different regions. The 16th piece may be viewed as an animation here to visualize it. I'll break down each region with an animation showing how it changes as a function of the ratio of the radius to the cube width and the resulting volume of the area.
The first region is defined by:
Here is a gif of the region:
The second region is defined by:
Here is a gif of the region:
The third region is defined by:
Here is a gif of the region:
The fourth region is defined by:
Here is a gif of the region:
The fifth region is defined by:
Here is a gif of the region:
Finally, all the regimes/regions may be combined into a python script which calculates the cube-sphere intersection volume. I should mention that I'm not that good at calculus and I think the two unevaluated integrals have analytic forms which I just can't find yet. That's one of the problems of doing integration by hand; you have to be better than me. I'm considering investing in a Mathematica license after doing these integrals. Here's the python code:























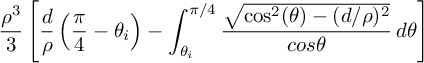

Very interesting what you did!
ReplyDeleteI was looking for something similar but... in N dimension and with the sphere that has its center in the cube but not necessarily coinciding with the center of the cube. After 2 years do you think it is even remotely possibile to generalize your results?
Probably just do importance sampling integration for that. Sorry it took me a year to reply...
DeleteThere is a little type in the expression of I4, it's pi/4 instead of pi/5. Good job anyway !
ReplyDeleteYup, thanks! It's correct in the Python code, but yes the equation is wrong.
Delete